Zalecane przeglądarki :FireFox, OPERA, GoogleChrome
Pomoc dydaktyczna. ver:10.1 : 03-2016 autor: Jan Kraus
Nowa wersja programu - nowe opcje:Liczby zaspolone poz.6 ,Interpolacja funkcjami sklejanymi poz.12 ,
Opereacje na macierzach w tym wartości i wektory własne poz. 11 ,
Rozklad macierzy na LU i macierz odwrotna poz. 9 .
Pakiet programów zawiera następujące składniki:
-
 Idź do: » »
Idź do: » »
Program to make graphs of functions of one variable y = f (x) » »
Program do robienia wykresów funkcji jednej zmiennej y=f(x).
» opis »
-
 Idź do: » »
Idź do: » »
Program to make graphs of functions of one variable y = f (x) plus full graphics » »
Program do robienia wykresów y=f(x) plus pełna grafika:




linie,wektory,okręgi,styczność,prostopadłość opisy itp.
Dla zaawansowanych wykres momentów gnących belki » opis »
-
 Idź do: » »
Idź do: » »
Program to make graphs of functions set equations parametric x = x (t) and y = y (t) » »
Program do robienia wykresów funkcji zadanej równaniami
parametrycznymi x=x(t) i y=y(t). » opis »
-
 Idź do: » »
Idź do: » »
A program for making graphs of functions in a polar r = r (x) » »
Program do robienia wykresów funkcji w układzie biegunowym r=r(x)
gdzie x kąt mierzony w radianach. » opis »
-
 Idź do: » »
Idź do: » »
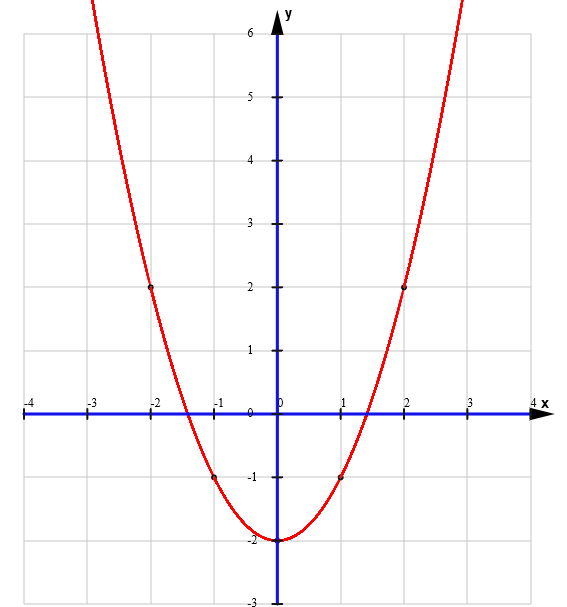
A program for analysis of a quadratic function » »
Program do analizy funkcji kwadratowej - ver beta /
-
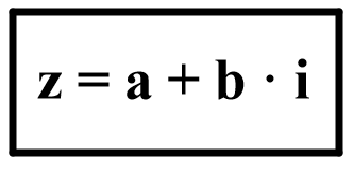 Idź do: » »
Idź do: » »
A program for demonstrations , operations on complex numbers » »
Program do demonstracji działań na liczbach zespolonych - ver beta /
-
 Idź do: » »
Idź do: » »
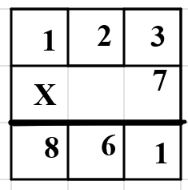
A program for multiple big integer numbers » »
Program do pismiennego mnozenia duzych liczb
-
 Idź do: » »
Idź do: » »
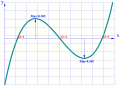
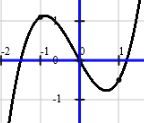
The equation for solving three-degree
Program do rozwiązywania równania 3-go stopnia
z graficzną interpretacją rozwiązań
-
 Idź do: » »
Idź do: » »
A square matrix inversion ,Cholesky , Crout & Dolittle LU Method » »
Program do odwaracania macierzy przez rozkład na LU
metodą Choleskiego , Crouta lub Doolittle.
Dla 3 x 3 mnemotechniczna demonstracja mnożenia macierzy
-
 Idź do: » »
Idź do: » »
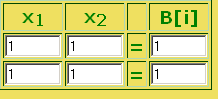
The program for solving a determined and overdetermined system of linear equations.
Program do rozwiązywanie określonego i nadokreślonego układu
równań liniowych oraz do wyznaczania macierzy odwrotnej,
w tej wersji do 9-ciu rownań.
-
 Idź do: » »
Idź do: » »
A Program to demonstrate the basic operations on matrices
Program do wykonywanie podstawowych operacji na macierzach
-
 Idź do: » »
Idź do: » »
A Program to demonstrate the spline type
Program do interpolacji typu sklejanego. Do wyboru
trzy stopnie funkcji interpolujacej - sześcienna,kwadratowa i liniowa. » opis »
-
 Idź do: » »
Idź do: » »
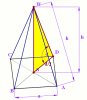
The program for drawing in parallel perspective, 3D blocks
Program do rysowania w perspektywie równoległej
różnych brył przestrzennych. » opis »
-
 Idź do: » »
Idź do: » »
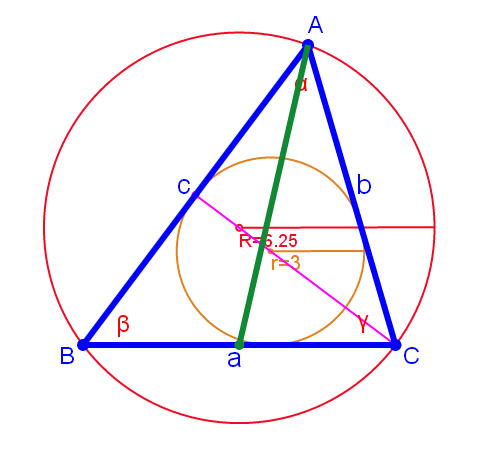
The program for solving triangles for different data » opis »
Program do rozwiązywania trójkątów
przy różnym sposobie ich określenia. » opis »
-
 Idź do: » »
Idź do: » »
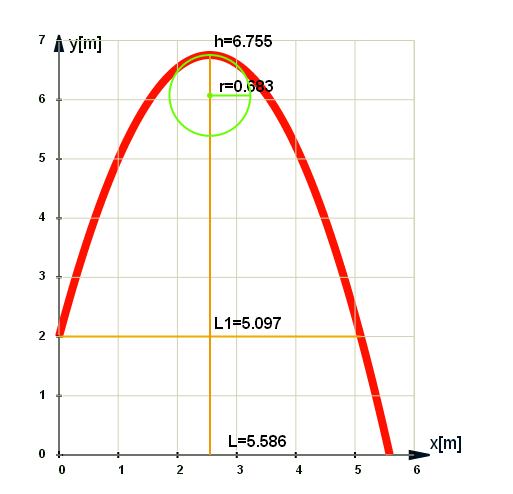
Program to make graphs and analysis diagonal and horizontal throw » opis »
Program do robienia wykresów i analizy
rzutu ukośnego, rzutu poziomego i swobodnego spadku. » opis »
-
 Idź do: » »
Idź do: » »
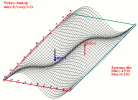
Program for drawing 3D graphs of functions of two variables z = f(x, y) or isoline » »
Program do rysowania wykresów funkcji dwóch zmiennych z=f(x,y) ,
do wyboru 3D lub poziomice. » opis »
-
 Idź do: » »
Idź do: » »
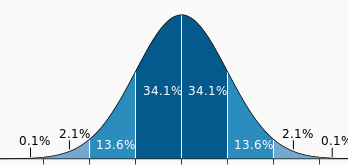
Gęstość i dystrybuanta prawdopodobieństawa ,
do wyboru rozkład normalny , chi kwadrat lub (t-Studenta NA) » opis »
-
 Idź do: » »
Idź do: » »
Continuous beam on an elastic substrate. »»
Program do obliczeń belki ciągłej na sprężystym podłożu
Program wyznacza ugięcia, kąty ugięć, momenty zginające, siły poprzeczne
i reakcje podporowe we w/w belkach
Dla studentów - przeczytaj info » opis » » opis »
-
 Idź do: » »
Idź do: » »
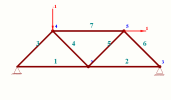
Software for the calculation of the grid plane
Program do obliczeń kratownicy płaskiej
statycznie wyznaczalnej i niewyznaczalnej na podporach stałych
z uwzglednieniem więzi kinematycznych .
[ dla studentów ] » opis »
-
 Idź do: » »
Idź do: » »
Software for the calculation of the flat frame
Program do obliczeń ramy płaskiej
z belkami obciążonymi siłami, momentami i obciążeniem ciągłym
liniowo zmiennym z uwzględnieniem więzi kinematycznych .
[ NOWA OPCJA dla studentów - przeczytaj ograniczenia ] » opis »
-
 Idź do: » »
Idź do: » »
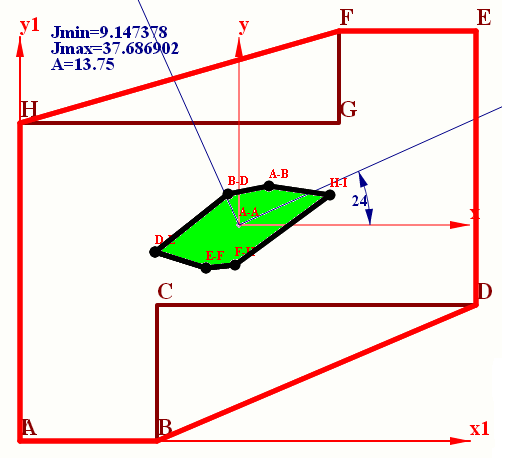
A program for calculating and plotting the core section stretching the eccentric beam.
Program do obliczania i wykreślania rdzenia przekroju
przy mimośrodowym rozciąganiu belki.
[ NOWA OPCJA dla studentów szkół technicznych ]
-
 Idź do: » »
Idź do: » »
Biblioteka gotowych rysunków do wykorzystania
z możliwością ich modyfikacji dla własnych potrzeb » opis »
-
 Idź do: » »
Idź do: » »
Tricky questions
Zadania z haczykiem
- uchwyt: koniec
- uchwyt: połowa
- uchwyt: przecięcie
- uchwyt: środek - okręgu
- uchwyt: ćwiartka - kwadrans
- uchwyt: styczny do okręgu
- uchwyt: prostopadły
-
Program do robienia wykresów funkcji jednej zmiennej y=f(x)
Przy pomocy tego programu można jednocześnie zrobić trzy wykresy
zaznaczając pole wyboru po prawej stronie opisu funkcji.
W przykładzie pokazano wykresy dwóch parabol i jednej prostej
stycznych do tych parabol.
Opcja może być przydatna w badaniu przebiegu funkcji
lub w pokazaniu składników szeregu Taylora:
lub szeregu Fouriera:
obrazujące, że suma kilku funkcji sinus i cosinus może dawać nową funkcję.
[f1(x)= 3.14*3.14/3-4*cos(x)+1*cos(2*x) ,
f2(x)= 3.14*3.14/3-4*cos(x)+1*cos(2*x)-4/9*cos(3*x) ,f3(x)=x^2
a=-3 b=3 il=6 y1=-1 y2=9 il=10]
Zachęcam do testów.
-
Program do robienia wykresów funkcji jednej zmiennej y=f(x)
Przy pomocy tego programu można jednoznacześnie zrobić trzy wykresy, podając ich przepis
plus pełna grafika: linie, wektory, okręgi,prostopadłość, prostokąty wielokąty itp
i zaznaczając pole wyboru po prawej stronie opisu funkcji.
Wykresy można uzupełnić o dodatkowe elementy takie jak:
okręgi, asymptoty, przedziały zmiennych, kąty itp.
Zwracam uwagę na linię komend w której przygotowalem przykład jej wykorzystania:
W lini komend można policzyć wartość wyrażenia stosując znak zapytania
przyklad: ? sin(pi/2) zwraca -1 UWAGA kąt liczony w prawo !
Uwaga nowa opcja [copy segment] [kopiuj odcinek linii] może zawieszać program
proszę ustawić kursor [w nowym oknie] w tej lini i nacisnąć [ENTER] Ten przypadek pokaże w przykładzie:
proszę wtedy nacisnąć klawisz ESCNowa opcja w lini komend: tabela zmienności funkcji:
F1 0 0 1 2 3 4 - wyrysuje tabelę dla funkcji f1(x), F2 dla f2(x), F3 dla f3(x)
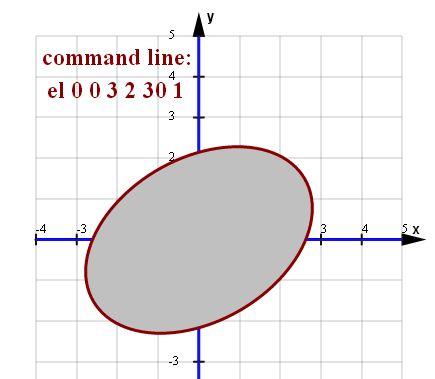
lewy dolny róg (0,0) argumenty 1 2 3 4W lini kommend dostępne jest polecenia rysowania elipsy:
el xs ys a b αlfa ver przykład:ver=0
el 0 0 3 2 30 0ver=1
el 0 0 3 2 30 1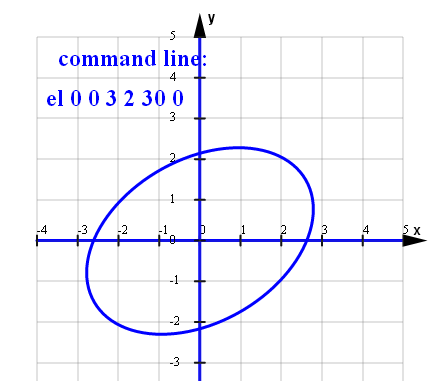
Oraz polecenie rysowania hiperboli w 3-ech wersjach - przyklady:
ver=0
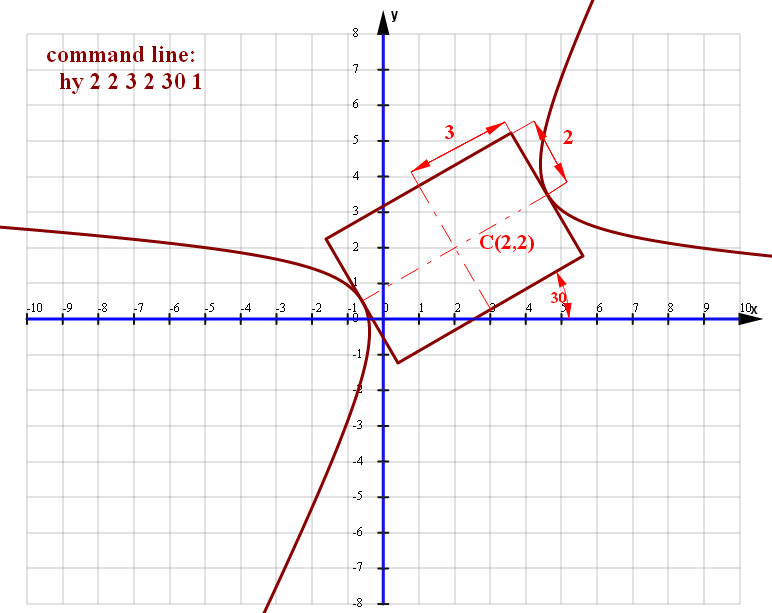
hy 2 2 3 2 30 0ver=1
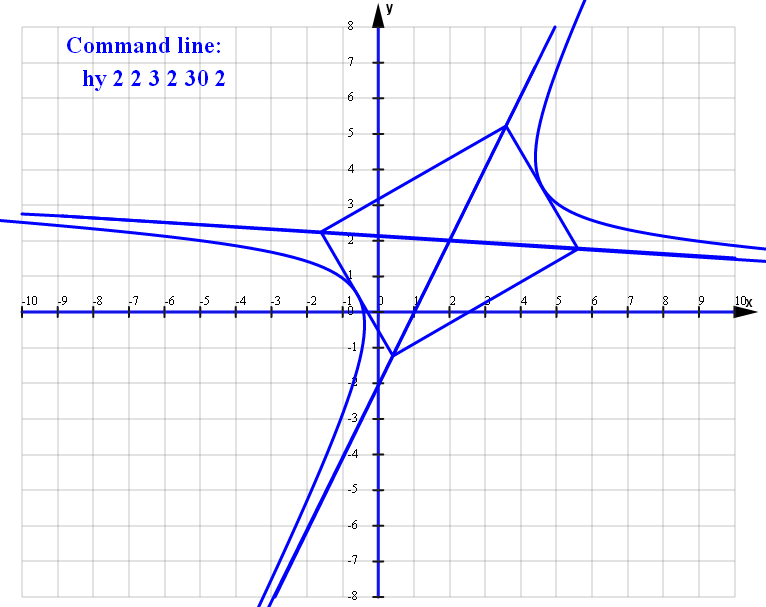
hy 2 2 3 2 30 1ver=2
hy 2 2 3 2 30 2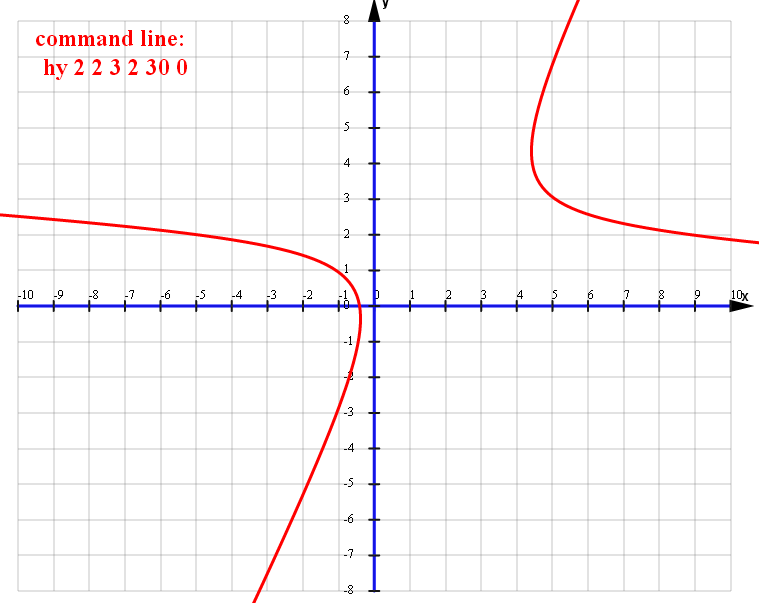
Możemy zrobić także tylko grafikę - w tym celu,
proszę usunąć wszystkie wybory funkcji lub w pytaniu jaki wykres wybrać [tylko grafika]
Tylko dla zaawasowanych funkcje:
- lnull(x,x1) zeruj po lewej stronie x1,
- rnull(x,x1) zeruj po prawej stronie x1,
Wykresy momentów i linia ugięcia belki - metoda Clebscha
Funkcja opisująca moment gnący w rozbiciu na 3 przedzialy:
dla 0<x<1 , 1<x<2 , 2<x<3 w tym celu stosuje funkcje:
lnull(x,1) lnull(x,2)
Mg(x)=(-x+2*(x-1)*lnull(x,1)-2*pow((x-2),2)*lnull(x,2))*rnull(x,3)
Funkcja rnull(x,3) [zeruj powyzej x=3], mnoży cały przepis aby zakończyc wykres dla x=3 .
Korzystając z równania linii ugięcia EJ*y''=-Mg(x) , zakładam EJ=1.
całkuje dwa razy w/w obliczam C1 i C2.
Otrzymane wykresy widać po akceptacji.
Kąt ugięcia i ugiącie są zerowe w miejscu utwierdzenia , tzn dla x=3.
Gdzie zeruje sie moment /czerwony wykres/ kąt ugięcia /niebieski/ ma extremum
PS. W/w metodę można zastosować do funkcji , której przepisy
podane są w kilku przedziałach
-
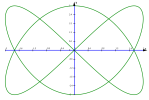
Program do robienia wykresów funkcji zadanej równaniami
parametrycznymi x=x(t) i y=y(t) Przy pomocy tego programu można zoobracoac np. Krzywe Lissajous
Opcja może byc przydatna do zobrazowania różnych ruchów w kinamatyce
np. rzut poziomy rzut ukośny wystarczy wtety przyjąć:
x(t)=t i t1=0 y(t)=h-1/2*g*t*t lub y(t)=Voy*t-1/2*g*t*t
Zachęcam do testów.
-
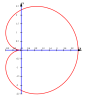
Program do robienia wykresów funkcji w układzie biegunowym r=r(x)
Przy pomocy tego programu można zobrazować różne ciekawe krzywe
gdzie x kąt mierzony w radianach
np. spirala czy kardioida (krzywa sercowa)
Ciekawe efekty daje funkcja
r=sin(4*x) lub np. r=cos(3*x)
Zachęcam do testów.
-
Program do rysowania w perspektywie równoległej
Przy pomocy tego programu można pokazać typowe bryły przestrzenne
różnych brył przestrzennych
w perspektywie równoleglej przy różnych ustawieniach kąta patrzenia.
W tej wersji zaimplementowano tylko bryły regularne proste.
Zachęcam do testów.
-
Program do rozwiązywania i rysownaia trójkątów
przy różnym sposobie ich określenia jak poniżej- bbb - 3 boki
- bkb - 2 boki i kąt pomiędzy nimi zawarty
- kbk - 2 kąty i bok pomiędzy nimi
- bbk - 2 boki i kąt naprzeciwko większego z nich
- bhk - bok i kąt naprzeciwko oraz wysokość do niego prostopadła
Zachęcam do testów.
-
Interaktywny program do obliczeń i rysowania sklejanej funkcji interpolacyjnej.
Daje to możliwosci sprawdzenia jak zaburzenie wartości w jednym węźle wpływa na nastepne.
Są do wyboru trzy funkcje i trzy stopnie funkcji interpolującej.
Przy zadaniu takich samych wartości dla wszystkich funkcji - można to zrobic np. przez RESET.
Mozna również załadować funkcje testową - przycisk po lewejj stronie pod rysunkiem. Teraz przy zadawaniu funkcji można zmieniać stopień funkcji inptepolujacej - przyciski typu radio,
i obserwować wszystko na jednym rysunku - np tak jak rysunek w opracowaniu M.Pazdanowskiego
Należy jeszcze zaznaczyc do rysowania fynkcjje f2(x) i f3(x), f1(x) rysuje się zawsze.
Zachęcam do testów.
-
Program do analizy rzutu ukosnego, poziomego i swobodnego spadku
Program oblicza i podaje następujące parametry rzutu:
- Równania ruchu x=x(t) y=y(t)
- Równanie toru y=y(x)
- Zasięg rzutu L
- Wysokość rzutu h
- Czas wznoszenia t1
- Czas opadania t2
- Przyspieszenie styczne
- Przyspieszenie normalne
- Promień krzywizny toru
Zachęcam do testów.
-
Program do wykresów funkcji dwóch zmiennych do wyboru 3D lub poziomice
Przy pomocy tego programu można pokazać wykres wybranej lub zadanej
funkcji dwóch zmiennych z=f(xy).
Uwaga program wysyła dużą ilość danych do serwera dlatego proszę o cierpliwość.
Na początek - dla testu - proszę wybrać dokłądnośc joko: [zgrubny]
Zachęcam do testów.
-
Program do demonstracji dystrybuanty i gęstości zmiennej losowej
Dla rozkładu normalnego,
przy pomocy tego programu można określić prawdopodobienstwo
podanego zakresu zmiennej losowej, lub dla zadanego zakresu
można okreslic jego prawdopodobienstwo.
Można również odczytac wartoćci funkcji
Moivre'a - Laplace'a F(x), f(x) dla zadanego argumentu
Dla rozkładu chi kwadrat można sprawdzić istotność przykładowej hipotezy zerowej H0.
Można zmienić opis i liczebność klasy - dla wlasnych potrzeb.
Jest mozliwość zmiany ilości klas - aby opisać inną hipotezę zerową
Brak jest jeszcze rozkladu t-Studenta .
Zachęcam do testów.
-
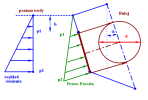
Program do obliczeń belki ciągłej na sprężystym podłożu
Program wyznacza ugięcia, kąty ugięć, momenty zginające ,siły poprzeczne
NOWA OPCJA
i reakcje podporowe w belkach statycznie wyznaczalnych i niewyznaczalnych opartych na:
- sprężystym podłożu
- podporach stałych
- dowolnej kombinacji wyżej wymienionych sposobów podparcia
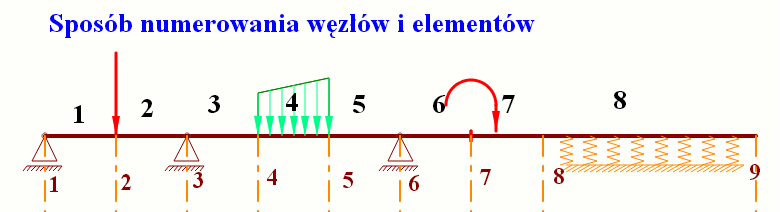
Belka jest podzielona na elementy przez:
patrz na rysunek powyżej
- obciążenia stałe [tkz węzłowe] siły i momenty (znak + na rysunku)
- obciążenia ciągłe , mogą byc liniowo zmienne
- podpory - więzy podporowe
- odpór podłoża
Aby przygotować dane:
Ponumeruj węzły idąc od lewego końca belki. Na rysunku 9
Ponumeruj elementy idąc od lewego końca belki. Na rysunku 8
Możliwe więzy podporowe :
1 Podpora przesuwna SP=1 2 Utwierdzenie przesuwne SP=2 3 Utwierdzenie całkowite SP=1 i SP=2
Uwaga na podporę nr 3 utwierdzenie całkowite.
W ilości podpór taką podporę należy policzyć dwa razy -
i na etapie wprowadzania danych należy
ją dodać jako sposób podparcia: SP=1 i SP=2 !!
Pozostałe informacje po uruchomieniu programu.
Zachęcam do testów.
-
Program do obliczeń kratownicy płaskiej
Program wyznacza rekacje podporowe i sily osiowe we wszystkich prętach kratownicy
NOWA OPCJA
Aby przygotowac dane :
Ponumeruj węzły
Ponumeruj pręty
Określ rodzaj podpór stałych i rodzaj więzi kinematycznych
Określ liczbę różnych materiałów [moduł sprężystości]
Określ liczbę różnych przekrojów [pole przekroju ]
Wpisz odpowiednie dane o które pyta program:
Pozostałe informacje po uruchomieniu programu.
Zachęcam do testów.
-
Program do obliczeń ramy płaskiej
Program wyznacza momenty ,siły poprzeczne, ugięcia i kąty ugięcia
Program w trakcie testowania
we wszystkich elemantach - belkach - ramy płaskiej:
Aby przygotować dane:
Ponumeruj węzły belki i ponumeruj belki.
Podaj wspólrzedne węzłow w prawoskretnym ukladzie wspólrzednych
patrz rysunek:
Na jednej belce jest możliwe obciążenie tylko jedną siłą skupioną P[Px,Py]
tylko jednym momentem skupionym i jednym obciązeniem ciągłym .
W przypadku innych obciążeń należy dodać dodakowy węzeł.
Wszystkie obciążenie należy podawać w globalnym układzie odniesienia.
Uwaga w zakresie obciążenia ciągłego
niedopuszczelne jest obciążenie siłą lub momentem !!
Opcja - deformacja - działa prawidłowo tylko dla prawidłowo dobranych
Pozostałe informacje po uruchomieniu programu.
stałych materiałowych moduł Younga oraz przekrój i moment bezwładności !!
UWAGA1! Dla danych testowych Piotra Plucińskiego przyjmij:
gdy jednostki wlączone E=0.001 A=1.5e5 J=3375
gdy brak jednostek: E=1 A=1.5e5 J=3375
UWAGA2! Dane opisujące ramę są przechowywane w sesji, i w przypadku:
bezczynności zostaną utracone po 25 minutach.
Zachęcam do testów.
-
Biblioteka gotowych rysunków do wykorzystania,
Przy pomocy tego programu - bazując na przygotowanym szablonie
z możliwością ich modyfikacji dla własnych potrzeb.
można przystosować rysunek dla własnych potrzeb.
Dostępne są wszystkie opcje modifikacji takie jak:- usunięcie lini,okręgu
- zmiana napisu,
- dodanie nowych elementow: linii,prostokątow,wielokoatów,okręgów i napisów
Polecam uwadze rysunek - ruch harmoniczny.
Dla lepszej czytelności proszę usunąć siatkę.
Zachęcam do testów.
- Wschody i zachody słonca / sunrises and sunsets
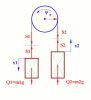
- Silnik 4-ro suwowy animacja / Engine 4-stroke animation
- Animacja- Rzut ukosny i poziomy / Diagonal and horizontal throw animation
-
Animacja - Rzuty ukosny lub poziomy analiza dwóch rzutów /
Two diagonal and horizontal throw animation
<<<<<<<<<<<<<<<<<<<<<***>>>>>>>>>>>>>>>>>>>>>>>
Każdy program ma zdefiniowane początkowe dane w celu pokazania swoich możliwości .
W tym celu należy zaakceptować przygotowane podpowiedzi.
Po uruchomieniu przykładu można wybrać opcję [zmień dane startowe]
i wpisać własne funkcje w przygotowane miejsce opisane jako f1(x),f2(x) i f3(x)
Bryły mogą mieć narysowane większość potrzebnych pomocniczych
linii takich jak np. promienie podstawy wysokości ścian bocznych itp.
W tym celu należy zaznaczyć odpowiednią opcję przed akceptacją.
Zbędne linie można usunąć korzystając z opcji [usuń] ikona w górnym menu,
po zakończeniu w/w należy wybrać [koniec usuń].
Wszystkie linie potrzebne do narysowania bryły są zapisane w pliku
typu *.plt z którego korzysta makro rysujące. Szczegóły podane są po uruchomieniu tej opcji.
Po usunięciu można dorysować potrzebne brakujące linie
korzystając z opcji [rysuj linię] w menu bocznym.
Można wybrać opcję lokalizacji punktu:
aby zwymiarowac wielkości liniowe proszę wybrać rysuj wymiar / wektor i narysuj go w dwie strony .
Można również umieścić dodatkowe napisy, korzystając z opcji pisz tekst,
należy wtedy podać współrzędne tekstu, wielkość liter i kąt nachylenia.
Ogólna uwaga do wykresów x(t) y(t) i uklad biegunowy:
Podnoszenie do potęgi należy zastąpić
funkcją pow(podstawa,wykładnik) lub wielokrotnym mnożeniem.
Np. 2^3 => pow(2,3)
y=pow(3,2) daje wynk: 9
Opis i przykłady uruchomienia konkretnych programów
Programy są w wersji "beta" i będą sukcesywnie dopracowywane
W sprawie uwag i pytań proszę pisać na mój mail.: kraus@l5.pk.edu.pl
Chętnie przeczytam opinie i krytyczne uwagi nt. programu
We are happy to read critical comments
