1. Przypadek "bbb". Patrz rysunek po prawej stronie DANE: a=16 b=8 c=20 Aby policzyć pole - policzę wysokość h
c 2 dwa razy z twierdzenia Pitagorasa
b
2 -(c-x)
2 =a
2 -x
2
b
2 -c
2 +2cx-x
2 =a
2 -x
2
b
2 -c
2 +2cx=a
2
Można zapisać tkz. uogólnione twierdznie Pitagorasa :2 =a2 +c2 -2·c·ac gdzie x=ac rzut a na c 2 =a2 +c2 -2·a·c·cos(β)
Znając x możemy z niebieskiego trójkąta policzyć wysokość
h
c 2 =a
2 -x
2
i następnie pole trojkąta jako P=1/2·c·h
c
Podstawiam dane : a=16 b=8 c=20
S=1/2·c·hc =1/2 · 20 · 6.079 = 60.795 [j2 ]
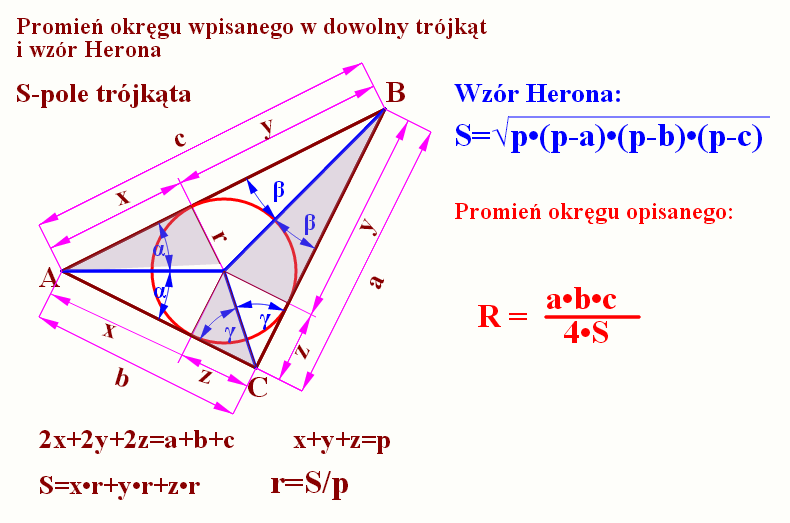
Inny sposób obliczenia pola to wzór Herona:
gdzie p to połowa obwodu
p=(a+b+c)/2=(16 + 8 + 20 )/2= 22
p·(p-a)·(p-b)·(p-c)=22 · 6 · 14 · 2 = 3696
S=√ 3696 = 60.795[j2 ]
Można również wykorzystać twierdzenie Carnota [ cosinusów ]
z jedynki trogonometrycnej:
S=1/2·a·c·sin(β)=1/2 · 16 · 20 · 0.38 = 60.795[j2 ] Obliczenie kątów i promieni okręgów opisanego i wpisanego.
Promień okręgu opisanego:
R=a·b·c/(4·S)=16 · 8 · 20/(4 · 60.795 ) = 10.527
Promień okręgu wpisanego:
r=S/p= 60.795 / 22 = 2.763
Z twierdznia Carnota policzone powyżej cos(β)=0.925 co daje:
β=arccos( 0.925 )= 22°19'53'' kąt α można policzyć podobnie jak kąt β z twierdzenia Carnota:
co daje:
α=arccos( 0.65)= 49°27'30''
kąt γ można policzyć z sumy kątów w trójkącie
γ=180-α-β= 108°12'35'' Obliczenie długości dośrodkowych
Wyprowadzenie wzoru umieściłem już we wcześniejszym
moim opracowaniu :
wybierz środek ciężkości
Tutaj załączam kopię tego opracowania:
Patrz rysunek obok.
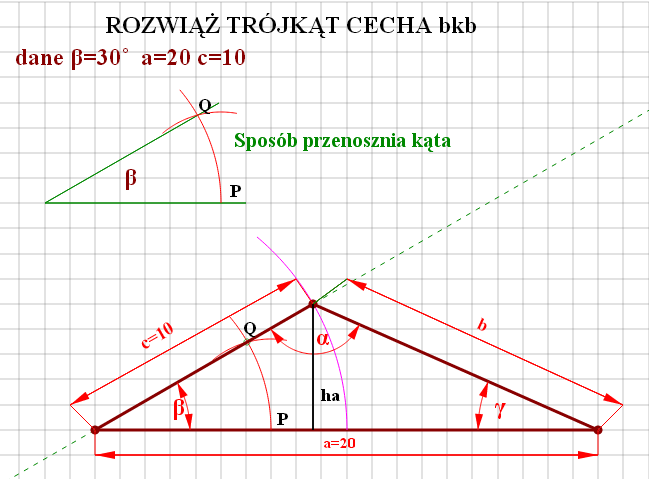
2. Przypadek "bkb" Patrz rysunek po prawej stronie DANE : a=20 beta=30 c=10
Policzę najpierw brakujący bok b. W tym celu zastosuje twierdzenie Carnota;
cos β=0.866
Podstawiam dane z rysunku obok:
Mając już bok "b" można zastosować wzory z przypaku 1-szego tj. bbb
do policzenia cosinusa kąta α
α=arccos(-0.5907)=126°12'21''
Dla takich danych łatwo policzyć pole trójkąta ze wzoru:
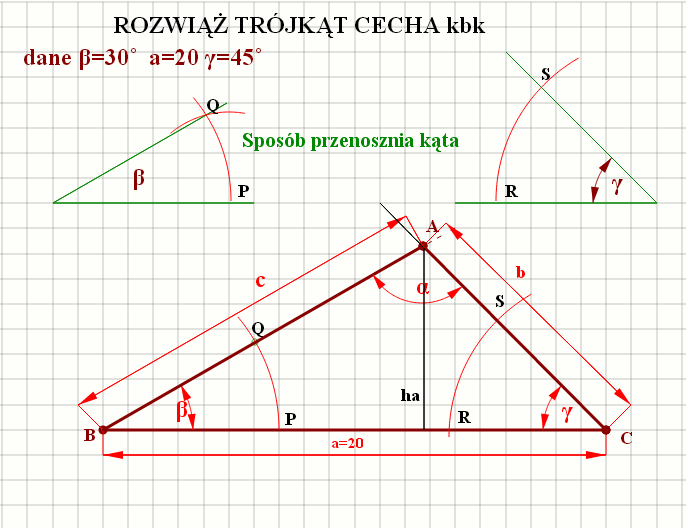
Kąt γ=180-α-β = 23°47'38'' , ale pokażę jednak jak można zastosować twierdzenie sinusów do policzenia kąta γ.
gdzie R - promień okręgu opisanego
Znając bok b oraz sin(β) możemy policzyć sinα i sinγ i nastepnie kąty: α i γ
Uwaga dla kąta rozwartego daje sinus kąta zewnętrznego
γ=23°47'38''
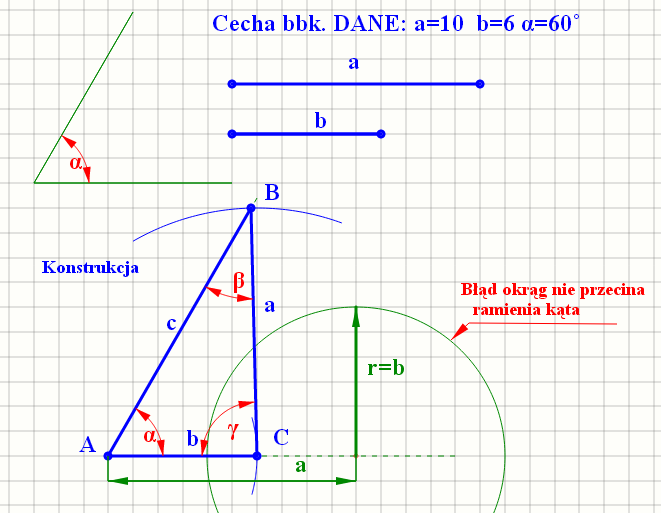
4. Przypadek "bbk" Dwa boki i kąt naprzeciwko wiekszego
DANE: alfa=60 a=10 b=6
Korzystając z twierdzenia sinusów policzę kąt β
0.5196 => β=31.3064
Kąt γ można policzyć z sumy kątów w trójkącie
γ=180-α-β= 88.694
Teraz korzystając z twierdzenia sinusów policzę bok c
Przy tych danych łatwo policzyć promień okregu opisanego:
Korzystąjąc z promienia R można policzyć pole trójkąta:
Pozostałe wielkości opisujące trójkąt można policzyć podobnie
jak w przypadku 1-szym bbb
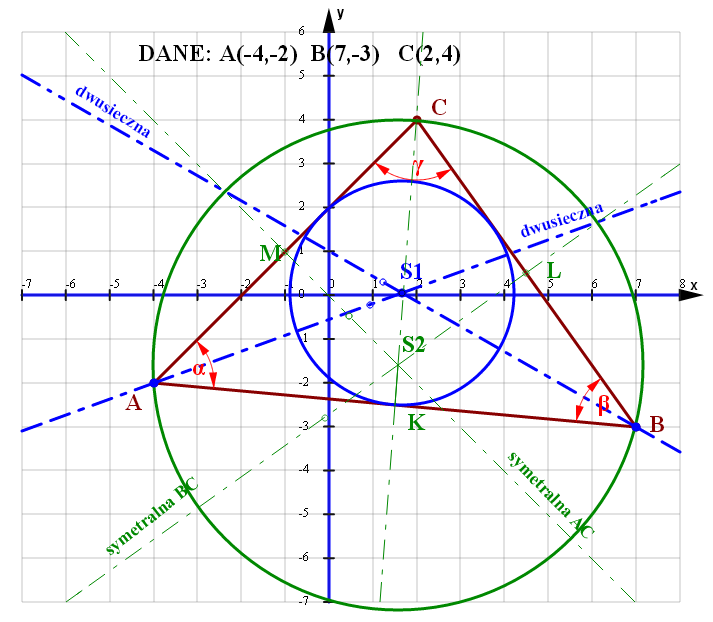
Patrz rysunek po prawej stronie, na którym widać współrzędne zadanych punktów trójkąta
DANE STANDARTOWE
DANE A(-4,-2) B(7,-3) C(2,4) Równania prostych w których zawierają się boki trójkąta W tym celu wykorzystam równanie pęku prostych .
Patrz moj help gotowe.php
Wybierz równanie pęku prostych
Wspólczynniki kierunkowe boków trójkąta:
mAB= -1/(11)=-0.091
mBC= 7/(-5)=-1.4
mAC= 6/(6)=1
Wyprowadze również równanie prostej przez dwa punkty
w postaci ogólnej; P1(x1,y1) i P2(x2,y2)
przy założeniu że prosta przechodzi przez punkt P(x1,y1)
Równanie potrzebne bedzie do obliczenia odleglości punktu od prostej
Przekształce równanie parametryczne cytowane powyżej
Po wymnożeniu ostateczna ogólna postać:
Równania ogólne boków trójkąta mają postać:
Długości boków policzę jako długość wektora
Równania wysokości i pole trójkąta **************
DANE A(-4,-2) B(7,-3) C(2,4)
Równania wyskości podobnie jak równania boków napiszę stosując równanie pęku prostych.
Wspólczynniki kierunkowe boków trójkąta obliczone powyżej wynoszą:
mAB= -1/(11)=-0.091
mBC= 7/(-5)=-1.4
mAC= 6/(6)=1
Z warunku prostopadłości obliczę współczynniki kierunkowe wysokości:
Patrz moj help gotowe.php
wybierz tanges kąta dwie proste
m
hc =-(11)/(-1)=11
m
ha =-(-5)/(7)=0.714
m
hb =-(6)/(6)=-1
Przeciecie wysokości wyznacza punkt zwany ORTOCENTRUM H( 1.833 , 2.167 ) Policze jeszcze długosci wysokości - wykorzystam wzór na odleglość punktu od prostej.
Wysokość ha jako odleglość punktu A od BC
ha= 8.37 a=8.602 ==> S=1/2*a*ha=36 Wysokość hb jako odleglość punktu B od AC
hb= 8.485 b=8.485 ==> S=1/2*b*hb=36 Wysokość hc jako odleglość punktu C od AB
hc= 6.519 c=11.045 ==> S=1/2*c*hc=36 Pole trójkata można policzyć jako połowę wyznacznika dwóch wektorów -
Miary kątów i funkcja cosinus DANE A(-4,-2) B(7,-3) C(2,4)
Aby policzyć miary kątów potrzebne są dwa wektory wychodzące z tego samego wierzchołka.
Policzę kąty alfa i beta a kąt gamma z sumy kątów w trójkacie.
Z wierzchołka A kąt alfa : α=50.194428907735 = 50°11'39'' Z wierzchołka B kąt beta : β=49.267893300291 = 49°16'4'' γ=80.537677791974 = 80°32'15''
Równania dośrodkowych ich długości i środek ciężkości DANE A(-4,-2) B(7,-3) C(2,4)
Potrzebne punkty K, L, M.
K(1.5 , -2.5) L(4.5 , 0.5) M(-1 , 1) Dośrodkowe dzielą sie w stosunku 1:2 liczac od boku trójkata. Równania symetralnych boków - środek i promień okręgu opisanego na trójkącie ABC Gdy symetralna pionowa błąd do poprawy
DANE A(-4,-2) B(7,-3) C(2,4) Środek okręgu opisanego leży na przecięciu symetralnych boków ,
w tym celu policzę współrzędne środków wszystkich boków. Punkty K, L, M.
K(1.5,-2.5) L(4.5,0.5) M(-1,1)
Policzę teraz współczynniki kierunkowe symetralnych boków
Z warunku prostopadlości wynika , Patrz moj help gotowe.php
tanges kąta dwie proste
mK=-(11)/(-1)=11 mL=-(-5)/(7)=0.714 mM=-(6)/(6)=-1
Przecięcie dwóch symetralnych wyznacza środek okręgu opisanego , patrz rysunek
symetralna AB: y=-(11/-1) • [x-(1.5)]+(-2.5)=11 • [x-(1.5)]+(-2.5)=
11 • x+(-19) symetralna BC: y=-(-5/7) • [x-(4.5)]+(0.5)=0.714 • [x-(4.5)]+(0.5)=
0.714 • x+(-2.714) Rozwiązanie w/w układu wyznaczy współrzędną środka S2 okręgu opisanego.
xS2=[-2.714 -(-19)]/[11-(0.714)]=1.583 ys2=-1.583
S2(1.583,-1.583),
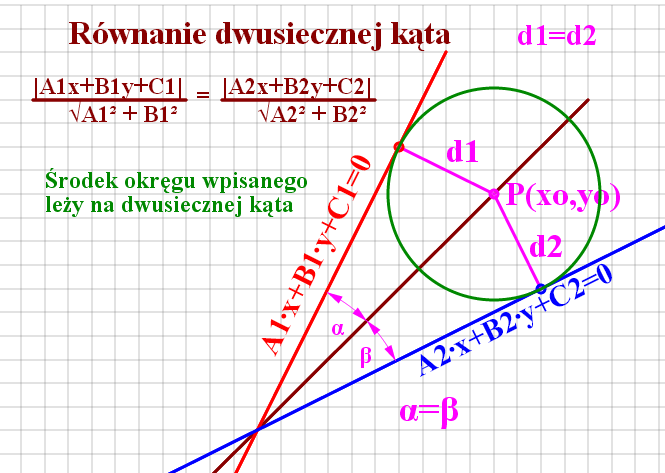
Równania dwusiecznych kątów - środek i promień okręgu wpisanego w trójkąt ABC
DANE A(-4,-2) B(7,-3) C(2,4) Równania dwusiecznych tylko kątów alfa i beta :
Przepiszę równania ogólne boków trójkąta obliczone powyżej
i zastosuję wzory widoczne na rysunku po prawej stronie
-------------------------------------------------------
-------------------------------------------------------
Po opuszczeniu modułu mamy 4 przypadki - należy wybrać Zobacz przykładowy rysunek
x=-6.425 y=4.697
Środek poza trójkątem- okrąg dopisany r=6.45
x=10.605 y=3.288
Środek poza trójkątem- okrąg dopisany r=6.589 x=1.673 y=0.054
Znając współrzędne środka okręgu wpisanego mogę obliczyć jego promień
korzystając ze wzoru na odleglość punktu od prostej - rysunek po prawej
okrąg wpisany xS1=1.673 yS1=0.054
x=0.479 y=-14.372
Środek poza trójkątem- okrąg dopisany r=11.916
 Patrz rysunek po prawej stronie, na którym widać współrzędne zadanych punktów trójkąta
Patrz rysunek po prawej stronie, na którym widać współrzędne zadanych punktów trójkąta Wysokość ha jako odleglość punktu A od BC
Wysokość ha jako odleglość punktu A od BC 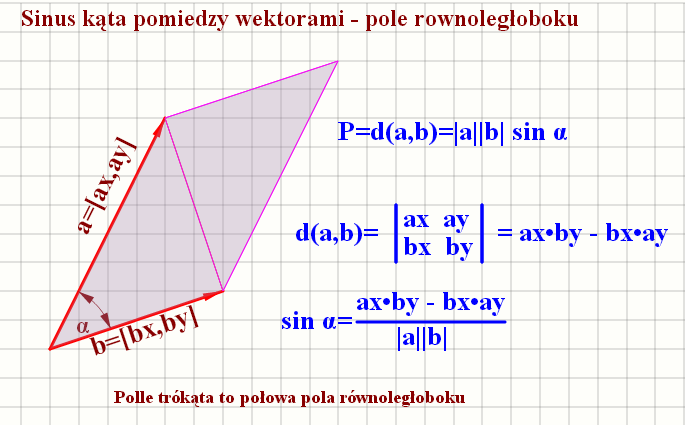
 Aby policzyć miary kątów potrzebne są dwa wektory wychodzące z tego samego wierzchołka.
Aby policzyć miary kątów potrzebne są dwa wektory wychodzące z tego samego wierzchołka.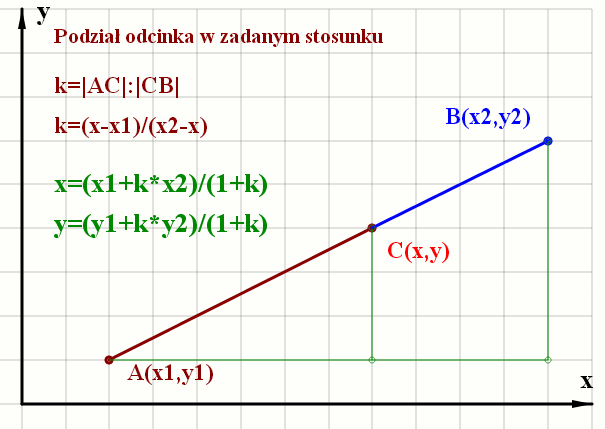 Dośrodkowe dzielą sie w stosunku 1:2 liczac od boku trójkata.
Dośrodkowe dzielą sie w stosunku 1:2 liczac od boku trójkata.