Program do interpolacji typu sklejanego
A Program to demonstrate the spline type [ver 2.3 03-2016 ]
Interpolacja - na podstawie opracowania M. Pazdanowskiego , Politechnika Krakowska Interpolacja przy pomocy funkcji sklejanych [ z angielskiego - typu spline ], polega na tym, że wielomian interpolujący jest tworzony oddzielnie dla każdego odcinka pomiędzy dwoma kolejnymi węzłami. Współczynniki wielomianów obowiązujących na poszczególnych odcinkach są wyznaczane tak, aby we węzłach zapewnić ciągłość nie tylko funkcji interpolującej ale także jej pochodnych do stopnia 1−n włącznie, jeżeli stopień wielomianu interpolującego jest równy n . Jedną z możliwych definicji wielomianu interpolacyjnego typu splajn jest, interpolacja funkcją 3-go stopnia :
Oznaczenia:
- p- numer przedziału / the number range
- n- numer wązła / node n=0,1,....p
- Δy- różnica funkcji do korekty / the difference functions for correction
- bp - współczynnik korekty w przedziale p / correction factor between p
- k - stopień funkcji splajn k=3 / degree spline function k = 3
Ogólna metoda wyznaczania funkcji:
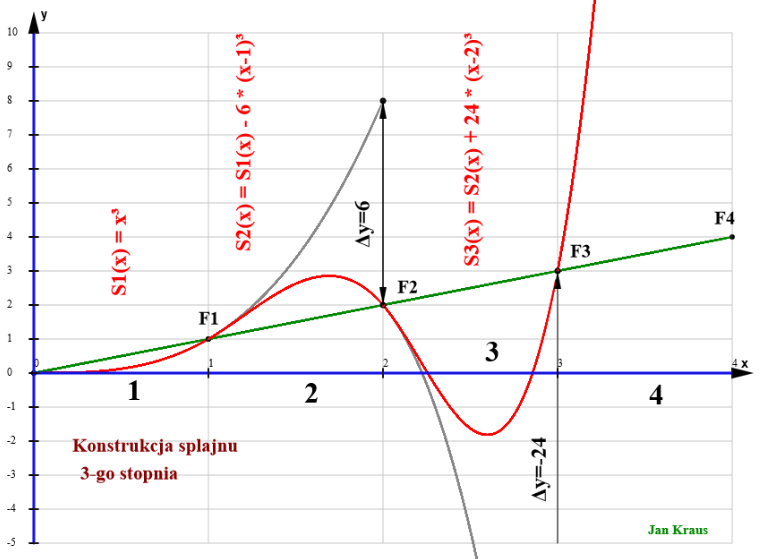
Funkcja podana w przedziale poprzednim nie "trafia"w końcowy węzeł następnego przedziału - dlatego należy wprowadzić korektę D(x)=bp*(x-xp-1)^3
współczynnik bp jest liczony na podstawie powstałej różnicy Δy- patrz rysunek powyżej.
Analogia do metody Clebscha - momentów gnących belki
gdzie:
X- współrzędne wewnątrz przedziału,
Xp-1 - współrzędna początku przedziału ,
(X - Xp-1) na początku przedziału jest równe zero - dlatego kerekta nie wprowadza nieciągłości funkcji
i nieciągłości pochodnej.