Rzut ukośny i poziomy

Zalecane przeglądarki :FireFox, OPERA, GoogleChrome

Rzut ukośny i poziomy / Diagonal and horizontal throw

Vo=10 alfa=60 yo=2 g=9.81

Strona będzie pokazywać sposoby obliczeń
parametrów określających rzut ukośny/poziomy:
wyniki będą pokazane w tabeli i jako wykresy lub jako animacja

Równania ruchu x(t), y(t)
Równanie toru y=y(x)
Prędkość chwilowa w zależnoaści od czasu V=V(t)
Zasięg [L] i wysokosc rzutu [h]
Tor rzutu wysoki i tor niski
Przyspieszenie styczne i normalne w zalazności od czasu at=at(t), an=an(t)
Promień krzywizny toru r=r(t)

Do określenia parametrów rzutu ukośnego należy podać:
patrz rysunek obok

Prędkość /Vo/ początkowa w [m/s]
Kąt rzutu /α/ z poziomem w stopniach
Wysokosć /yo/ nad poziomem od której rozpoczyna się rzut
Przyspieszenia ziemskie /g/ lub na zadanej planecie

Poziom yo wprowadzilem aby można opisać rzut poziomy wówczas yo musi byc większe od zera yo>0 !!
Rzut ukośny to złożenie dwóch ruchów:
- jednostajnego ruchu poziomego z prędkością Vox=Vo*cosα=const
- jednostajnie zmiennego ruchu pionowego z prędkością początkową Vox=Vo*sinα
i z przspieszeniem ziemskim g [lub występujacym na zadanej planecie ]

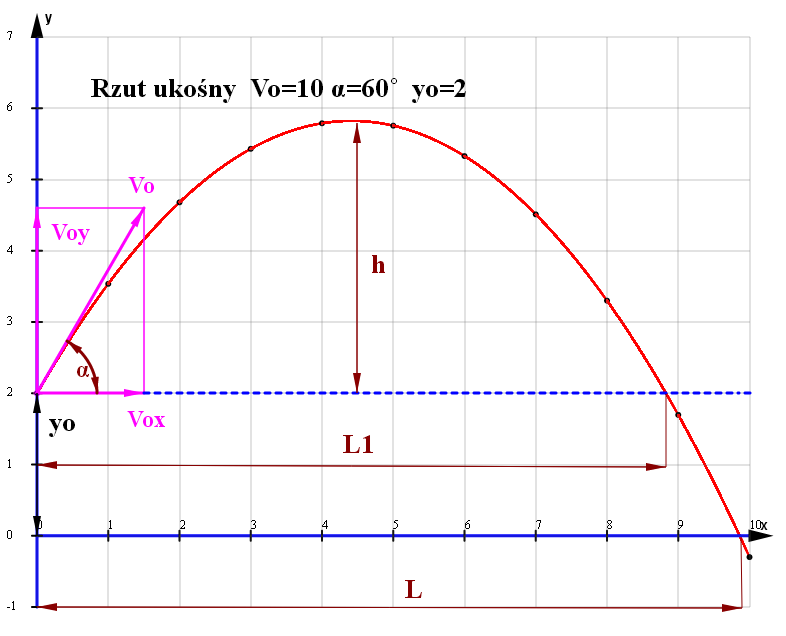
Przykładowe dane : Vo=10[m/s] α=60˚ yo=2[m]

1. Określenie równań ruchu

$x(t)=V_{ox} \cdot t=V_o \cdot t \cdot cos \alpha \\ y(t)=y_o + V_o \cdot t \cdot sin \alpha - \frac{1}{2}gt^2 }$

Są to równania parametryczne określające położenie punktu materialnego
w układzie wspólrzędnych xy

2. Określenie równania toru y=y(x)

W tym celu z równań ruchu należy wyrugować parametr czasu "t"

$x(t)=V_o \cdot t \cdot cos \alpha \Rightarrow \ \ \ t=\frac{x}{V_o \cdot t \cdot cos \alpha }$

$y(x)=y_o + V_o \cdot \frac{x \cdot sin\alpha}{V_o \cdot cos\alpha} -g \frac{x^2}{2 \cdot V_o^2 \cdot cos^2 \alpha}$

$y(x)=y_o + x \cdot tg \alpha -x^2 \cdot \frac{g}{2 \cdot V_o^2 \cdot cos^2 \alpha}$

3. Prędkość chwilowa V=[Vx , Vy]

Prędkość chwilowa w kierunku poziomym jest równa prędkości
początkowej w tym kierunku więc:

$V_x(t)=Vo \cdot cos \alpha =const$

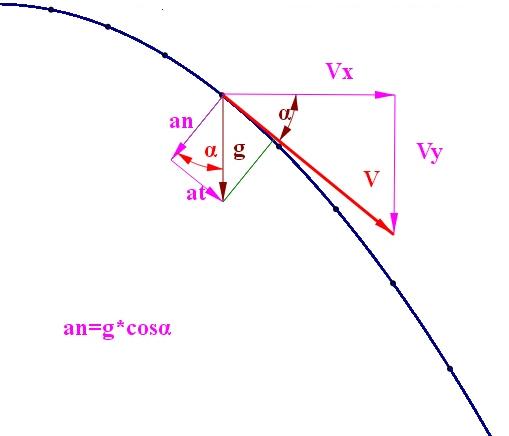
Prędkość chwilową w kierunku pionowym określa wzór:

$V_y(t)=Vo \cdot sin \alpha - g \cdot t$

Długość wektora prędkości chwilowej dla czasu t można obliczyć jako :

$V(t)=\sqrt{ V_x^2 + V_y^2}$

4. Określenie zasięgu /L/ i wysokosci /h/ rzutu

Zadanie to można rozwiązać na dwa sposoby:
1. Korzystając z równań ruchu
2. Korzystając z równania toru

Ad.1
należy najpierw policzyć czas ruchu t=t1+t2
gdzie:
t1=czas ruchu w górę, czas wznoszenia - do momentu gdy Vy=0
t2=czas ruchu w dól, czas opadania - do momentu gdy y=0

$V_y(t)=V_o \cdot sin \alpha -g \cdot t =0 \Rightarrow \ \ \ t1=\frac{V_o \cdot sin \alpha}{g }=$ 0.8828 [s]

wysokość rzutu

$h=y_o + V_o \cdot t_1 \cdot sin \alpha -\frac{1}{2}g \cdot t1^2 \Rightarrow$

$h=y_o + \frac{V_o^2 \cdot sin^2 \alpha}{g}-\frac{V_o^2}{2g}\cdot sin^2 \alpha =y_o + \frac{V_o^2 \cdot sin^2 \alpha}{2g} =$ 5.8226 [m]

Czas t2 to czas swobodnego spadku z wysokości h

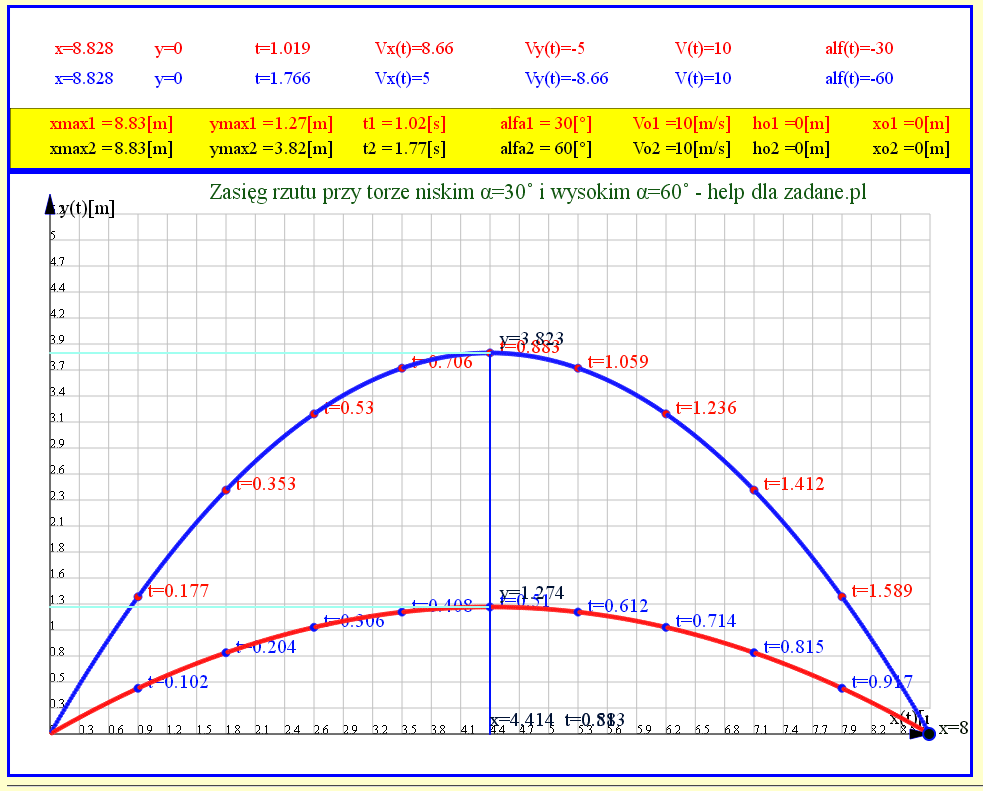
Jezeli yo=0 to t2=t1= 0.8828 [s] wówczas

$L1=x(2 \cdot t1) \ \ \Rightarrow L1=\frac{2\cdot V_o^2 \cdot sin \alpha \cdot cos \alpha}{g} =\frac{V_o^2 \cdot sin 2\alpha}{g} =$ 8.828 [m]

Łatwo zauważyć że dla zadanej prędkości początkowej zasięg jest największy gdy α=45°

Warto zauważyc takze że stosunek wysokości rzutu do jego zasięgu zależy tylko od kąta rzutu

$h/L=\frac{1}{4} \cdot tg(\alpha) \Rightarrow h=L \ \ gdy \ \ tg \alpha=4 \, \ \alpha=75.964^o$

5. Tor rzutu wysoki i tor niski patrz rysunek po prawej stronie

Najpierw przypomnienie z trygonometri sin(180°-α)=sin(α)
Dla lepszego zrozumienia popatrz na mój help gotowe.php wybierz koło trygonometryczne

Jeżeli za kąt α podstawimy do wzoru na zasieg 90-α to otrzymamy:

$L=\frac{V_o^2 \cdot sin 2 \cdot (90-\alpha)}{g} =\frac{V_o^2 \cdot sin(180- 2 \cdot \alpha)}{g}=\frac{V_o^2 \cdot sin 2\alpha}{g}$

Widać że zasiegi są równe.
Należy jednak zauważyć ze czasy rzutu są różne,
bo składowe poziome predkości sa różne.
Dla toru wysokiego składowa pozioma
jest mniejsza więc czas rzutu jest większy,
a dla toru niskiego składowa pozioma jest większa więc czas rzutu jest mniejszy. Widać to na rysunku obok gdzie wpisano współrzedną czasu .
Tu warto zauważyć ze w zadaniach w których jest dany zasięg
i predkość początkowa a mamy obliczyć
maksymalną wysokość rzutu to otrzymamy dwie odpowiedzi.

Sposob rozwiazania: Dane Vo=10[m/s] L=8,83[m]

OBL. y=h_max=?

$L=\frac{V_o^2 \cdot sin 2\alpha}{g} \ \Rightarrow sin(2 \alpha)=\frac{L \cdot g}{V_o^2} =A=6,867 \ \ \Rightarrow \\ A^2=4 \cdot sin^2 \alpha \cdot cos^2 \alpha \\$

$4u^2-4u + A^2=0 \ \ gdzie \ \ u=sin^2 \alpha \\$

$u_1=\frac{1}{2} \cdot \left(1-\sqrt{1-A^2} \right)=0,25} \ \Rightarrow sin^2 (\alpha)=0,25$

$u_2=\frac{1}{2} \cdot \left(1 + \sqrt{1-A^2} \right)=0,75} \ \Rightarrow sin^2(\alpha)=0,75 \\$

$h_{niski}=\frac{V_o^2 \cdot\sin^2 \alpha}{g}=1,275$

$h_{wysoki}=\frac{V_o^2 \cdot\sin^2 \alpha}{g}=3,822 \\$

Jezeli yo>0 wówczas:

$h=\frac{g \cdot t2^2}{2} \Rightarrow t2=\sqrt{\frac{2 \cdot h}{g}}=$ 1.0895 [s]

Dla danych z rysunku :

$t1 + t2=1.9723 [s] \ \Rightarrow$ $L=x(t1 + t2)=x(1.9723) =$ 9.8617 [m]

Ad.2 z równania toru
$y_o + x \cdot V_o \cdot tg \alpha -x^2 \cdot \frac{g}{2 \cdot V_o^2 \cdot cos^2 \alpha}=0 \ \Rightarrow$

$x \left(x \cdot \frac{g}{2 \cdot V_o^2 \cdot cos^2 \alpha} - V_o \cdot tg \alpha \right)=y_o$

Jezeli yo=0 wówczas:

$x_1=0 \ \vee \ x_2=L1=\frac{V_o^2 \cdot sin 2\alpha}{g}$

Jezeli yo>0 policze dla konkretnych danaych z równania kwadratowego

$x^2 \cdot \frac{g}{2 \cdot V_o^2 \cdot cos^2 \alpha} - x \cdot V_o \cdot tg \alpha + y_o=0 \ \Rightarrow$

$A=\frac{g}{2 \cdot V_o^2 \cdot cos^2 \alpha}=$ 0.1962

$B= -V_o \cdot tg \alpha =$ -1.7321

$C =-y_o=$ -2

$A \cdot x^2 + B \cdot x + C=0 \ \Rightarrow$

$\Delta=$ 4.5696 x1=-1.0337 x2=L=9.8617

6. Określenie przyspieszenia stycznego i normalnego

Zdefincji: Przyspieszenie styczne jest styczne do toru tzn. ma kierunek prędkości
a przyspieszenie normalne jest prostopadłe do kierunku prędkości
Całkowite przyspiesznie jest przyspieszeniem ziemskim. Więc można zapisać:

$\vec g= \vec {a_t} + \vec {a_n}$

Patrz rysunek po prawej stronie
$a_n=g \cdot cos \alpha \ \ ale \ cos \alpha=\frac{V_x}{V} \ \Rightarrow \ a_n=\frac{g \cdot V_x}{V}$

Dla najwyzszego punktu tzn. dla ymax=h V=Vx tzn an=g

Analogicznie:

$a_t=g \cdot sin \alpha \ \ ale \ sin \alpha=\frac{V_y}{V} \ \Rightarrow \ a_t=\frac{g \cdot V_y}{V}$

7. Określenie promienia krzywizny toru

Aby okreslić promień krzywizny należy wykorzystać defincję przyspieszenia normalnego.

$a_n=\frac{V^2}{r} \Rightarrow r=\frac{V^2}{a_n}=\frac{V^3}{g \cdot V_x}$

Zalecane przeglądarki :FireFox, OPERA, GoogleChrome